|
|
|
|
|
|
|
|


Cet article ayant pour unique objectif de découvrir le principe et les spécificités de l'injection électronique essence, l'approche utilisée sera différente d'un dossier traitant un type d'injection en particulier, afin de mettre en valeur les exigences et les objectifs auxquels tout système doit répondre. Si l'architecture de cet article ne vous semble pas judicieux, que certains points vous semblent confus, incomplets, voir faux, n'hésitez pas à me faire part de vos réactions ou questions.
Introduction_
Le passage du carburateur à l'injection essence, mécanique puis électronique, s'est avéré indispensable pour respecter les normes de pollution de plus en plus sévères au cours des années 90, et a permis une évolution importante du fonctionnement du moteur à piston alternatif.
Afin de réaliser les enjeux apportés par cette technologie, il est nécessaire de comprendre tout d'abord le processus de combustion du mélange air-essence dans la chambre de combustion.
Le mélange combustible_
Le mélange combustible est composé de deux éléments essentiels : le carburant (l'essence), qui va développer une énergie calorifique, et le comburant (le dioxygène de l'air), qui va permettre cette combustion. (On peut jeter une allumette dans un récipient rempli d'essence, l'essence liquide ne brûlera pas, mais seulement une partie des vapeurs qui se trouvent à sa surface).
Pour qu'il y ait combustion parfaite - c'est à dire qu'à la fin de la combustion il ne reste ni essence ni dioxygène - il faut que les éléments soient correctement dosés, c'est ce qu'on appelle le dosage stoechiométrique. Ainsi la combustion complète du mélange dioxygène + essence produit de l'eau, du dioxyde de carbone, et de l'énergie provenant de la fission des molécules d'octane.
Posons l'équation chimique :
Remarque : L'essence étant composée principalement d'octane, on la représentera par C8H18 (formule de l'octane).
Equation (non équilibrée) de la combustion : C8H18 + O2 => CO2 + H2O
Il faut maintenant équilibrer l'équation, afin qu'il y ait le même nombre d'atomes de chaque côté de la flèche (en chimie rien ne se perd, tout se transforme). Il suffit de compter le nombre d'atomes à gauche et à droite de la flèche.
| Nbre d'atomes à gauche | Nbre d'atomes à droite | |
|---|---|---|
| Carbone C | 8 |
1 |
| Hydrogène H | 18 |
2 |
| Oxygène O | 2 |
3 (2 + 1) |
Pour équilibrer on ne peut pas changer la quantité d'atomes dans les molécules (le petit chiffre placé derrière chaque atome), par contre on peut changer le nombre de molécules, en rajoutant un chiffre devant, auquel cas on multiplie l'ensemble des atomes. Exemple en rajoutant un 8 devant CO2: 8 CO2 = 8 atomes de carbone C + 16 atomes d'hydrogène H.
Equation équilibrée : 1 C8H18 + 12,5 O2 => 8 CO2 + 9 H2O
En ajoutant les coefficients ci-dessus, on obtient donc :
| Nbre d'atomes à gauche | Nbre d'atomes à droite | |
|---|---|---|
| Carbone C | 8 |
8 |
| Hydrogène H | 18 |
18 (9 x 2) |
| Oxygène O | 25 (12,5 x 2) |
25 ( 8 x 2 + 9) |
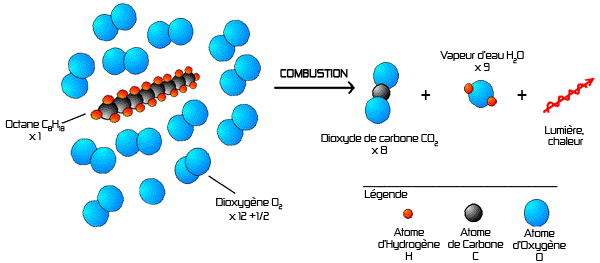
La combustion d'1 mole d'octane (à ne pas confondre avec molécule !) nécessite donc 12,5 moles de dioxygène pour produire exactement 8 moles de dioxyde de carbone et 9 moles d'eau.
L' atome est un élément infiniment petit qui mesure environ 1 Å (angström), soit 0, 000 000 000 1m ! Il est composé d'un noyau (constitué de neutrons et de protons) et d'un nuage ou gravitent des électrons sur différents niveaux. La molécule est un groupe d'atomes liés entre eux. La molécule du dioxyde de carbone se compose d'un atome de carbone et de deux atomes d'oxygène.
La mole est une unité, définissant une quantité de 6.023 x 1023 atomes (soit 602 300 000 000 000 000 000 000 atomes), appelé nombre d'Avogadro. En chimie, c'est une référence qui permet de calculer la masse des molécules à l'échelle humaine (une mole de carbone a une masse de 12g).
Chaque mole d'atomes a une masse précise, appelée masse molaire ou masse atomique, que l'on retrouve dans le tableau périodique des éléments établi par Mendeleïev.
D'après ce tableau : C = 12 g/mol ; H = 1 g/mol ; O = 16 g/mol.
On peut donc connaître la masse d'une mole d'octane C8H18 : 8 x 12 + 18 x 1= 114 g.
Il nous faut maintenant calculer la masse de l'air. Dans l'équation nous avons 12,5 moles de dioxygène, soit 12.5 moles d'air puisque le dioxygène n'est pas séparé de l'azote dans l'admission. (L'air que nous respirons n'est pas composé de 100% d'oxygène, mais d'environ 20% de dioxygène O2 et de 80% de diazote N2.)
Masse d'une mole d'air (O2+ 3.76 N2) : 2 x 16 + 3.76 x 2 x 14 = 137.28 g
Masse d'air nécessaire pour brûler une mole d'octane : 12.5 x 137.28 = 1716 g
Au final il faut donc 1716 g d'air pour 114 g d'essence, soit 1g d'essence pour 15.1 g d'air.
Dans la pratique, la valeur de référence utilisée sera 1 g d'essence pour 14.7 g d'air (l'essence ne contenant pas 100% d'octane, mais également de l'heptane et des additifs). La limite d'incombustibilité (mélange trop riche) est de 1/8, la limite d'inexplosivité (mélange trop pauvre) de 1/28.
La maîtrise de la combustion repose avant tout sur le respect de ce dosage, qui conditionne la puissance, la pollution et la consommation. La première difficulté est la vaporisation de l'essence dans l'air, puisque l'essence à l'état liquide ne permettrait pas de respecter ce dosage. Il est donc indispensable que le carburant soit uniformément réparti dans l'air, c'est à dire que le mélange soit homogène, afin que le dosage soit respecté en tout point du mélange.

|
|
|
|
|
|
|
|